In this article, we are going to learn about different types of decimals and how to use them in a number of ways. Decimal is an important chapter of NCERT class 7 maths.
Decimals are a unit of measurement that includes the numbers 0.1, 1/10, and so on. They are used to describe amounts that are smaller than whole numbers decimal points (or decimal points notation) is a way of writing decimals in your math papers and textbooks.
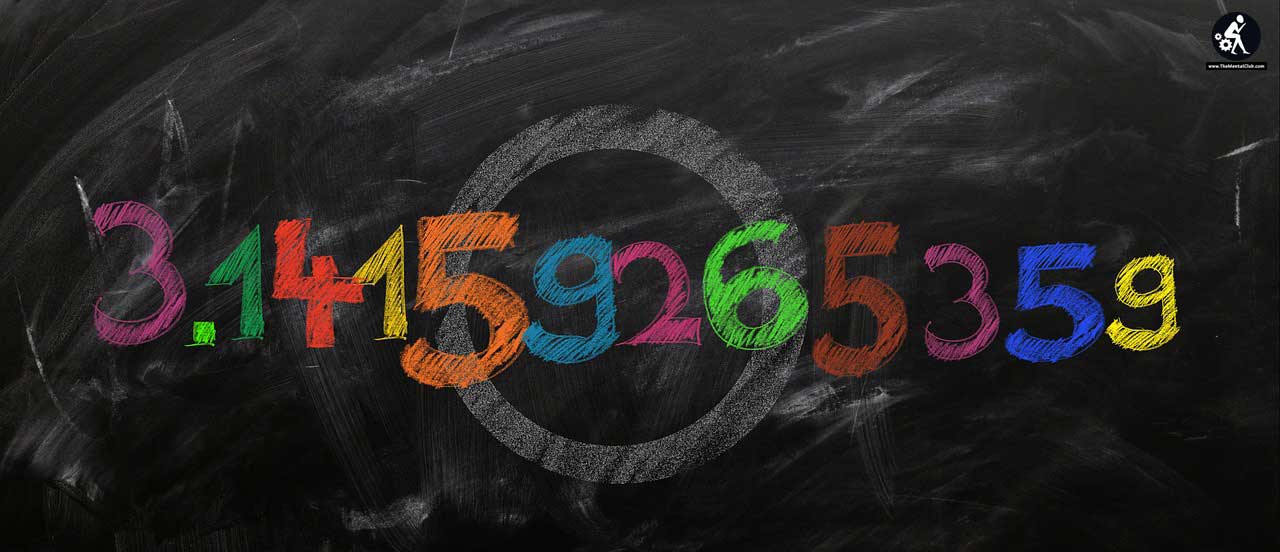
To understand what a decimal is, let’s take a look at an example. Suppose you want to buy a pack of gum at the store. You can’t just buy one pack – you have to buy two packs of gum. To buy two packs of gum, you would need to use two decimal points after the number “five.” This means that the number “five” would be written as 5.5 in standard notation.
In math, we often need to use decimals to multiply and divide numbers. For example, suppose you want to multiply two numbers: 8 × 9. In standard notation, this would be written as 8 × 9 using just digits (no punctuation). However, if we wanted to write it in decimals, we would write it as .89999999 × 9. This means that the number 8 would be multiplied by .89999999 and the number 9 would be multiplied.
How do you write a decimal number?
To write a decimal number, you need to use the symbol “.” followed by the number you want to write as a decimal. For example, to write 3.14, you would use the symbol “3.14.”
The definition of a decimal
A decimal is a number that is divided into tenths. For example, 1.5 is a decimal because it is equal to 1.5 (one and a half). Decimals can also be expressed as a fraction (1/10), as in 0.50.
The numeral system we use today evolved from the Roman numeral system. This system used Roman numerals (I, II, III, IV, V), which were only able to represent numbers up to 10. So, for example, the number 5 would be written as IIII. To represent numbers up to 100, another system was needed. This new system was developed by the Greeks and consisted of symbols like π (pi) or λ (lambda). These symbols represented different mathematical concepts, like area or volume.

Today, we still use decimals in our everyday lives. For example, when someone tells you that they have bought a car that costs $22000, you would understand that they have purchased two thousand two hundred and thirty units of currency (decimal).
Examples of decimal numbers
- Decimals can be used to represent a range of numbers.
- Decimal numbers are useful when dealing with numbers that are too small to be represented by whole numbers, or when more precision is needed.
- Decimal numbers can also be used in financial calculations.
- For example, if someone wanted to purchase a product for $10.99, they would use the decimal 10.99 rather than the number 10.
- In general, decimals are easier to work with than whole numbers, since they can be expressed in smaller chunks and are easier to remember.
Decimals and Fractions
- Decimals and fractions are two of the most common mathematical concepts. They both deal with numbers that are smaller than whole numbers.
- Decimals are just like whole numbers, but they have a decimal point ( . ) in the middle. For example, 2.5 is a decimal that means 2 plus .5.
- Fractions are also just like whole numbers, but they have a fractional point in the middle. For example, 1/2 is a fraction which means 1 divided by 2.
- You can use decimals and fractions to solve equations and problems. For example, if you want to find the total number of cars in a parking lot, you could use the equation 3 + 4 = 7 and solve for x to get the total number of cars in the parking lot: 7 cars.
- Decimals and fractions can also be used to describe quantities in prose. For example, if someone tells you that there are 25 cookies in a jar, you can say “There are three-quarters of a dozen cookies in the jar.”
Practice Problems
One way to learn decimals is to practice problems. There are a lot of problems available online, as well as in textbook chapters. Work through a few problems every day, and you will be on your way to being a confident decimal user.

Here are a few tips for solving decimal problems:
- Look at the problem carefully. Decimals are often written in fractions, so it is important to understand what the numerator and denominator are before starting to solve the problem. Infinity Learn provides the best
- Break the problem down into smaller pieces. Often, we can solve decimals by breaking them down into smaller parts. For example, if you are trying to find the value of 7÷4, divide 7 by 4 first and then solve for the quotient (3).
Conclusion
In this article, we learned about decimals and how to use them in everyday situations. We also explored how to convert fractions to decimals, and vice versa. By the end of the article, you should have a good understanding of what decimals are and how they can help you with your math problems.